電卓アプリ Numiで!難しい計算もMacで簡単にやろう

本記事ではMac上で難しい計算をして手書きをやめたい人に向けて、Numiの「基本的な使い方」と「応用的な使い方」の2点を解説していこうと思います。

Numiとは
Numiは単位・関数・変数・単位変換などの機能が備わったMac向けの電卓アプリになります。
Numiの最大の特徴は計算式を上から順番に記述していくというところです。通常の電卓では計算過程がわかりづらく、複雑な計算は手書きでやっている方も多いと思います。
Numiでは計算過程がわかりやすく記述でき、複雑な計算もMac上で簡単にできるようになっています。

基本的な使い方
計算を始めよう
計算を始めるときには「+」を押して開始します。

タイトルをつけよう
先頭行にはタイトルをつけておきます。するとリストから見つけやすくなるので、つけておくのがおすすめです。
# 1の段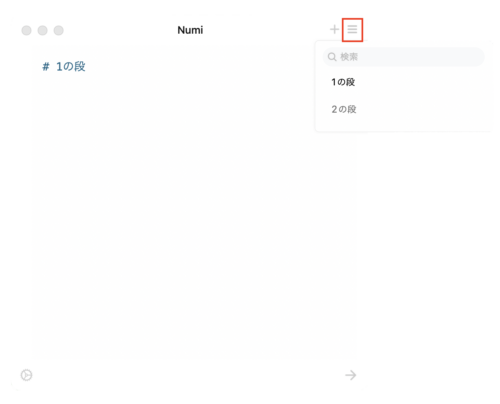
計算式を入力しよう
計算式を記入して計算を進めていきます。計算式は演算子の記号(+, −, ×, /)と数値(1,2,3,4,5,6,7,8,9)を利用して組み立てます。
# 1の段
1 * 1
1 * 2
1 * 3
1 * 4
1 * 5
1 * 6
1 * 7
1 * 8
1 * 9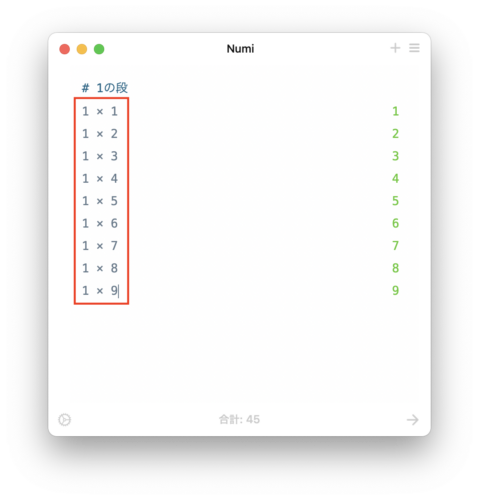
計算結果を確認しよう
計算式を入力したら、計算式の右側に計算結果が表示されます。計算結果をクリックするとコピーができるようになっているので必要に応じてコピーできます。
# 1の段
1 * 1 = 1
1 * 2 = 2
1 * 3 = 3
1 * 4 = 4
1 * 5 = 5
1 * 6 = 6
1 * 7 = 7
1 * 8 = 8
1 * 9 = 9
応用的な使い方
Numiには通常の電卓にはない数値変換や関数や変数などの応用的な機能をサポートしています。それぞれ順番にどのような機能があり何ができるのか解説していきます。
計算結果の集計
sumやavgで記入した計算式の計算結果の合計値・平均値を求められます。
記述方法
| 種類 | 記述例 |
|---|---|
| 合計値を求める | sum |
| 平均値を求める | avg |
動作確認
10
20
30
100 + 200
300 - 400
sum
avg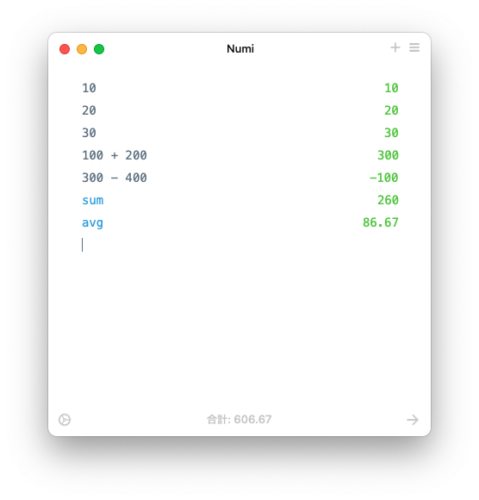
タイムゾーン変換
timeまたはnowで現在のタイムゾーンにおける現在時刻を取得できます。また「先頭に場所を記載するか」「inのあとに場所を記載すると」タイムゾーン指定で現在時刻を取得できます。
記述方法
| 種類 | 記述例 |
|---|---|
| 現在時刻(現在のタイムゾーン) | now, time |
| 現在時刻(タイムゾーン指定) | <場所> now, <場所> time , now in <場所>, time in <場所> |
動作確認
now # JAPAN
now in london
now in united states
time # JAPAN
time in london
time in united states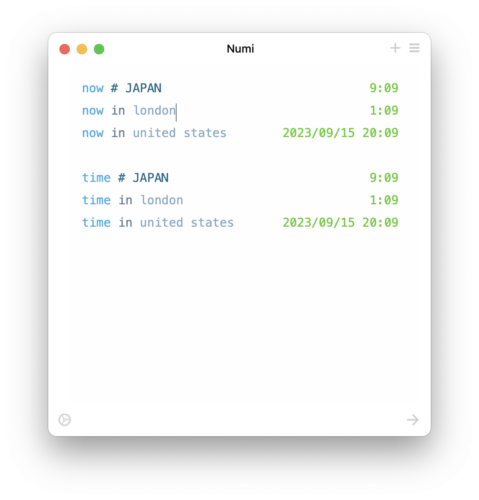
演算子
足し算・引き算・掛け算・割り算・べき乗などの計算のための演算子が用意されています。各計算の演算子として複数の記号が用意されているものがありますが、どの記号を利用しても計算可能になっています。
記述方法
| 種類 | 記号 | 記述例 |
|---|---|---|
| 足し算 | +, plus, and, with | <数字> + <数字> |
| 引き算 | -, minus, subtract, without | <数字> minus <数字> |
| 掛け算 | *, times, multiplied by, multiplied | <数字> multiplied by <数字> |
| 割り算 | /, divide, divide by | <数字> / <数字> |
| べき乗 | ^ | <数字> ^ <数字> |
| ビット演算子 AND | & | <数字> & <数字> |
| ビット演算子 OR | | | <数字> | <数字> |
| ビット演算子 XOR | xor | <数字> Xor <数字> |
| 左シフト | << | <数字> << <数字> |
| 右シフト | >> | <数字> >> <数字> |
| 剰余 | mod | <数字> mod <数字> |
動作確認
1 + 2
2 - 3
3 * 4
4 / 2
2 ^ 2
0xff & 0xf0
0xf0 | 0x0f
0xf0 & 0xff
0x0f << 4
0xf0 >> 4
8 mod 7
数値
2進数・8進数・16進数での数値表記ができます。0b・0o・0xを数値の先頭につけることで、2進数・8進数・16進数の数値で計算ができます。
記述方法
| 種類 | 記号 | 記述例 |
|---|---|---|
| 2進数 | 0b | 0b<数値> |
| 8進数 | 0o | 0o<数値> |
| 16進数 | 0x | 0x<数値> |
動作確認
0b1110 + 0b0001
0o7777 - 0o0707
0x8000 * 0x0002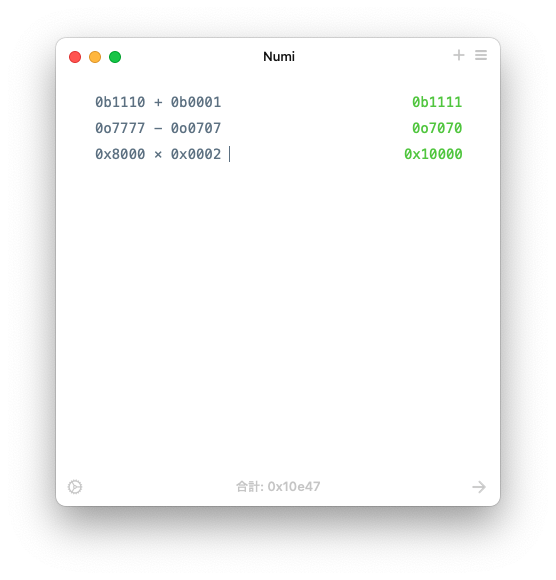
通貨
米ドルやユーロ、円などの通貨表記ができます。通貨表記を利用して通貨の加算・減算・パーセント計算ができます。※ Numiでは通貨レートを一日数回更新するらしいです、そのため最新の通貨レートで計算が可能です。
記述方法
| 種類 | 記号 | 記述例 |
|---|---|---|
| 米ドル | $, USD | $<数値>, <数値>USD |
| ユーロ | €, CAD | €<数値>, <数値>EUR |
| 日本円 | ¥, YEN | ¥<数値>, <数値>YEN |
動作確認
$10 - ¥500
€10 - ¥500
$10 - €10
10USD - 500YEN
10EUR - 500YEN
10USD - 10EUR
パーセンテージ
パーセンテージの加算・減算・比較の計算ができます。そのため通貨と併用して、金額の計算をすると便利です。
記述方法
| 種類 | 記述例 |
|---|---|
| <金額>の<数値>%の価格を求める | <数値>% of <金額> |
| <金額>の<数値>%の価格を足した価格を求める | <数値>% on <金額> |
| <金額>から<数値>%引いた価格を求める | <数値>% off <金額> |
| <金額1>は<金額2>の何パーセントであるか求める | <金額1> as a % on <金額2> |
| <金額2> は<金額1>の何パーセントであるか求める | <金額1> as a % off <金額2> |
動作確認
10% of ¥1000
10% on ¥1000
10% off ¥1000
¥100 as a % on ¥1000
¥100 as a % off ¥100
変数
=を利用して変数を定義することができます。変数として定義した値は他の計算式上で利用することが可能です。
記述方法
| 種類 | 記述例 |
|---|---|
| <数値>を<変数名>として変数定義する | <変数名> = <数値> |
| <計算式>の計算結果を<変数名>として変数定義する | <変数名> = <数値> + <数値> |
動作確認
x = 1
y = 1 + 2
z = x + y
定数
定数としてはパイ(π)とエクスポネンシャル(e)が用意されています。定数は計算式上で利用することが可能です。
記述方法
| 種類 | 記述例 |
|---|---|
| パイ(π) | PI |
| エクスポネンシャル(e) | E |
動作確認
PI
E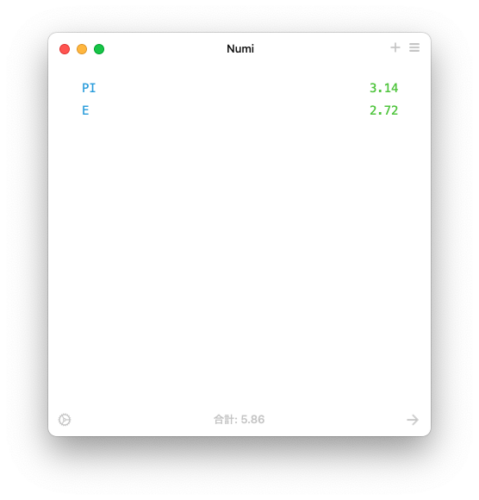
関数
数学の計算で用いられる関数が用意されています。これらの関数を駆使すると一般的な数学の計算式の計算結果を求められます。
記述方法
| 種類 | 記述例 |
|---|---|
| <数値1>の<数値2>乗根を求める | root <数値2> (数値1) |
| <数値>の平方根を求める | sqrt <数値> |
| <数値>の立方根を求める | cbrt <数値> |
| <数値>の絶対値を求める | abs(<数値>) |
| <数値1>を底とする<数値2>の対数を求める | log <数値1> (<数値2>) |
| <数値>の自然対数を求める | ln <数値> |
| <数値>の階乗を求める | fact <数値> |
| <数値>の焦点を丸める(四捨五入する) | round <数値> |
| <数値>以上の最小の整数値を求める | ceil <数値> |
| <数値>以下の最大の整数値を求める | floor <数値> |
| sin<数値>を求める | sin <数値>° |
| cos<数値>を求める | cos <数値> ° |
| tan<数値>を求める | tan <数値> ° |
| arcsin <数値>を求める | arcsin <数値> |
| arccos <数値>を求める | arccos <数値> |
| arctan <数値>を求める | arctan <数値> |
| sinh <数値>を求める | sinh <数値> |
| cosh <数値>を求める | cosh <数値> |
| tanh <数値>を求める | tanh <数値> |
動作確認
root 2 (8)
sqrt 16
cbrt 8
abs(-4)
log 2 (10)
ln 3
fact 5
round 3.45
ceil 3.76
floor 2.56
sin 90°
cos 180°
tan 45°
arcsin 1
arccos 0.5
arctan 1
sinh 3
cosh 9
tanh 11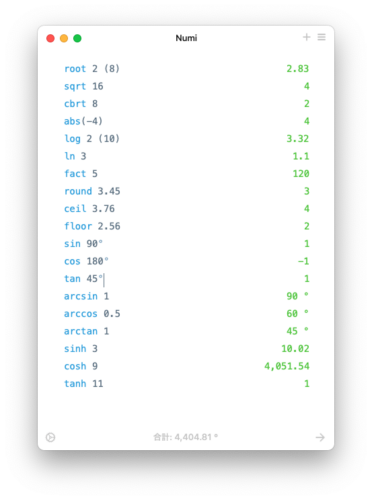
おわりに
本記事では主要なNumiの機能について解説をしました。Numiにはまだこの記事で紹介していない機能がありますのでもっと複雑な計算をやりたいという方はこちらのNumi公式のガイドを確認してみても良いかなと思います。